

The function \(f\) need not be defined at \(x=c\). Although this notion is intuitive, we will give a precise definition of the limit of a function and we will relate the definition with limits of sequences. As you may recall, a function \(f\) has limit \(L\) at a point \(c\) if the outputs \(f(x)\) are arbitrarily close to \(L\) provided the inputs \(x\) are sufficiently close to \(c\). To understand the idea of limit solved the examples with the help of constant, difference, and sum rules in detail.You are familiar with computing limits of functions from calculus. In this article, we discussed the definition of a limit and the basic rules of the limit such as product, sum, difference, and quotient. Lim X→-2 G(X) = 14 is the solution of X 2 – 3X + 4 at x = -2. Step 4: Apply the constant and identity rule and also simplify.Lim X→3 G(X) = 4 is the solution of X 2 – 5 at x = 3.įind the solution of the given function by the limits formulas, X 2 – 3X + 4 at x = -2. Step 4: Apply the constant, and identity rule and also simplify.
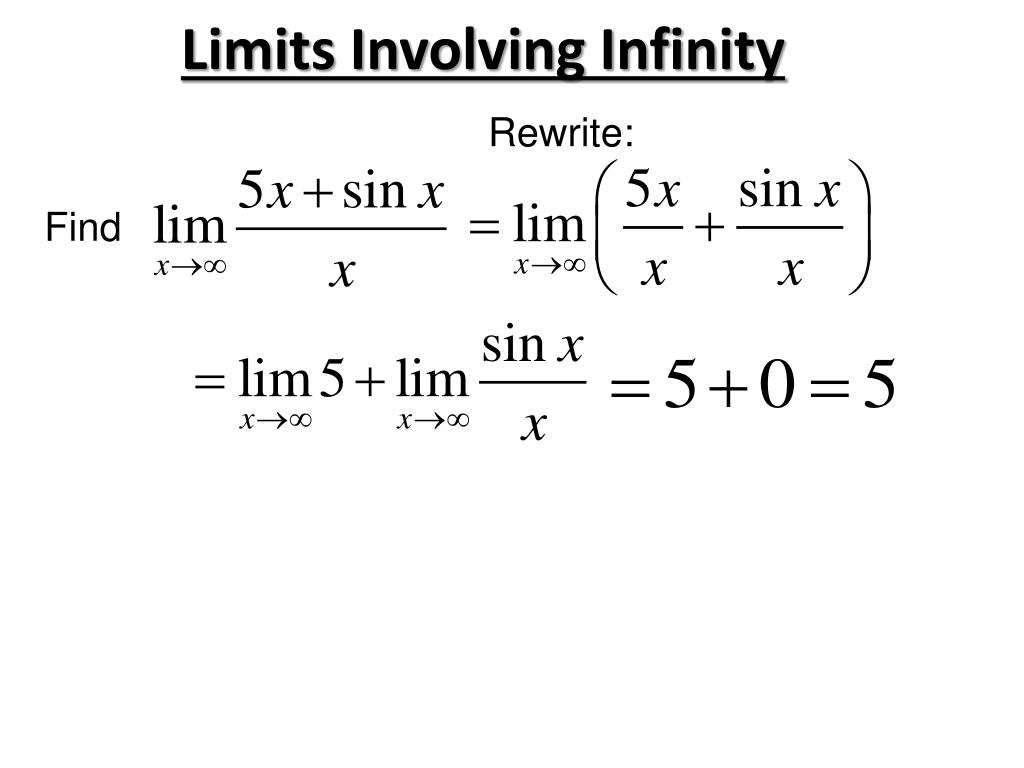

DEFINITION OF LIMIT CALCULUS EXAMPLES HOW TO
In this section, we’ll discuss the different examples to understand how to find the limit of a function.įind the solution of the given function by the limits formula x 2 – 5 at x = 3. Exponential Rule: The limit of the exponential function (f(X) = e X) as “X” approaches “c” then the limiting value is “e c”.Power Rule: The limit of a power function (f(X) = X n, where n is a positive integer) as “X” approaches “c” is equal to c n.That is, if Lim X→c (f(X)) = L and Lim X→c (g(X)) = M (where M ≠ 0), then Quotient Rule: The limit of the quotient of two functions is equal to the quotient of their limits (the denominator is not zero).If Lim X→c (f(X)) = L and Lim X→c (g(X)) = M, then Product Rule: The limit of the product of two functions is equal to the product of their limits.That is, if Lim X→c (f(X)) = L and Lim X→c (g(X)) = M, then Difference Rule: The limit of the difference between two functions is equal to the difference of their limits.Sum Rule: The limit of the sum of two functions is equal to the sum of their limits.Identity Rule: The limit of the identity function (f(X) = X) as “X” approaches “c” then its limiting value is “c”.Constant Rule: The constant function’s limiting value is identical to that of the constant itself.In this section, we discussed the basic rules of limits. It is used to prove many theorems in calculus and is performed many developments in modern analysis of mathematics and engineering. This definition is important because it provides a way to describe the behavior of functions as their input values approach a certain point.

“δ” represents a positive number that suggests how close the input values “X” to “c” are in order for the function values with “ε” of the limit “L”. In this definition, ε represents a positive number that specifies how the function values are nearer to the limit L. If for every ε > 0, there exists a δ > 0 such that, Let g(X) be a function defined on an interval that is open and contains the point “c,” perhaps with the exception of “c” itself. The extended definition of a limit is defined as: The extended definition of a limit involves the concept of neighborhoods and epsilon-delta definitions. It also has practical applications in fields such as physics and engineering. Limits are played a crucial role in calculus and mathematical analysis, and they are used to define important concepts such as continuity, derivatives, and integrals. The limit can exist even if the function is not defined at c or if it is defined differently at c. This notation indicates that we are interested in the behavior of g(X) as “X” gets closer and closer to “c”, but not necessarily equal to c. Where “L” is the limiting value of the function.


 0 kommentar(er)
0 kommentar(er)
